Í venjulegum rafmagnsvír rekast rafeindirnar stöðugt á óreglur í kristallagrindinni. Af meðaltali ferðast þær einungis örfáa nanómetra eða minna milli árekstra. Þær sveima því hægt um vírinn þó rafboðinn um hann berist með ógnarhraða. Leiðni vírsins er óháð lögun hans, en er háð hitastigi og hreinleika hans.
Ekki er ekki hægt að nota þessa mynd til þess að lýsa leiðni víra og hálfleiðara í minniskubbum og örgjörvum ef breidd þeirra fer að nálgast meðalfjarlægð milli árekstra. Um nokkurn tíma hafa eðlisfræðingar unnið að rannsóknum á mjög hreinum hálfleiðurum þar sem meðalvegur milli árekstra getur numið allmörgum mikrómetrum. Leiðni um þannig kerfi er orðin háð lögun þess og staðsetningu óreglna í því.
Leiðni er flókið fyrirbæri sem eðlisfræðingar á sviði þéttefnisfræði hafa glímt við alla síðustu öld, bæði í tilraunum og líkanagerð. Enn eru mörg óleyst vandamál og sífellt eru gerðar nýjar og óvæntar uppgvötanir.
Hér ætla ég að segja frá rannsóknum okkar á leiðni nanókerfa. Ég mun reyna að segja söguna á einfaldan og myndrænan hátt. Jöfnur verða sýndar án þess að hver stiki og breyta verði skýrð þegar úr þeim má lesa upplýsingar um samhengi eðlisfræðilegra fyrirbæra.
Hugsum okkur langan grannan vír. Rafeindir ferðast ótruflaðar eftir honum, en í miðju hans rekast þær á óreglu, aukamætti.
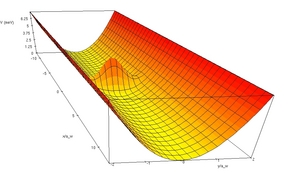
Breidd vírsins er á bilinu 10 - 200 nm samanborið við 90 - 130 nm sem tíðkast í smárásum 2004 - 2005, en við gerum ráð fyrir því að vírinn sé úr ákaflega hreinum GaAs hálfleiðara þannig að bylgjulengd rafeindanna sé ekki smá miðað við breidd vírsins. Vírinn er búinn til á mörkum AlGaAs einangrara og GaAs hálfleiðara og hæð hans er það lítil miðað við breidd að nægjanlegt verður að ímynda sér hann sem tvívítt rafeindakerfi. Þvert á vírinn skulum við hugsa okkur að hægt sé að hafa einsleitt segulsvið. Það myndi ekki gerast inni í minniskubbi, en í tilraunum er hægt að nota segulsviðið til þess að greina enn betur hvað gerist inni í vírnum. Rannsóknir okkar eru grunnrannsóknir sem beinast að því markmiði.
Til þess að lýsa hreyfingum rafeindanna inni í vírnum verður að nota skammatfræði. Jafna Schrödingers fyrir rafeindir sem koma t.d. inn í kerfið frá vinstri með fastri orku E verður hlutafleiðujafna í x-y-sléttunni. Við höfum áhuga á sístæða fyrirbærinu, það er, hvernig leiðnin breytist með orkunni E ef við hugsum okkur stöðugan straum rafeinda koma inn í kerfið frá vinstri og fara út úr því til hægri eða vinstri (því greinilega munu sumar rafeindir endurkastast af óreglunni í miðjum vírnum). Hreyfijafnan er því hlutafleiðujafna í tveimur breytum fyrir líkindadreifingu rafeindanna í kerfinu. Hlutafleiðujafna tengir eiginleika líkindadreifingarinnar í punkti (x,y) við dreifinguna í næsta nágrenni. Þessa jöfnu fyrir staðbundna eiginleika líkindadreifingarinnar ásamt jaðarskilyrðum (rafeindirnar koma úr einni átt og komast ekki langt til hliðar út úr vírnum) má leysa með aðferðum sem byggjast á endanlegri bútun eða mismunaaðferðum. Lausnin er þá byggð upp frá einhverjum punkti með því að nota upplýsingarnar sem felast í hlutafleiðujöfnunni.
Þetta er ekki sú aðferð sem við notum. Hér væri heppilegra að nota svo kallað fall Greens til þess að leita víðfeðminnar lausnar. Óregluna í miðju kerfinu viljum við geta mótað eftir þörfum. T.d. höfum við áhuga á að setja lítinn eða stóran hring inn í vírinn. Hugsum okkur rafeind sem kemur inn í vírinn. Ástandi rafeindarinnar er lýst sem bylgju með hraða v eða skriðþunga k. Hægt er að búa til fall Greens G(r) sem lýsir því hvernig innbylgjan veldur útbylgju í punkti r=(x,y) eftir að rekast á örgranna óreglu Vsc í vírnum í punkti r'=(x',y').
Í tvívíðri sléttu er útbylgjan hringbylgja sem streymir í allar áttir, en í vírnum okkar safnast útbylgjan saman vegna vírsins í þætti sem streyma að lokum til hægri eða vinstri frá árekstrarstað. Til þess að skoða áreksturinn við flóknara mætti eins og hring verðum við að summa upp útbylgjurnar frá sérhverjum punkti hringsins
Þetta er ekki alveg rétt lausn því sumar rafeindir rekast oftar á og því þurfum við að reikna út útbylgjuna frá árekstrarmættinu fyrir heildarbylgjuna en ekki bara fyrir innbylgjuna. Heildarbylgjan er summa inn- og útbylgju
Þar með erum við komin með víðfeðma jöfnu, heildisjöfnu, sem inniheldur allar upplýsingar hlutafleiðujöfnunar ásamt jaðarskilyrðunum. Jafnan er víðfeðm vegna þess að hún tengir saman alla punkta x-y-sléttunar. Hún er óbein því stærðin sem við viljum finna kemur fyrir báðum megin við jafnaðarmerkið, en það er einmitt eiginleiki heildisjafna. Þær bíta í halann á sér eða betur sagt við sjáum úr uppbyggingu þeirra að lausnin verður sjálfsamkvæm. Hún getur lýst síendurteknum árekstrum og því gæti rafeind dvalist um sinn í árekstrarmættinu áður en hún færi aftur út úr kerfinu.
Heildisjafnan inniheldur sömu upplýsingar og hlutafleiðujafnan með jaðarskilyrðum og þó hægt sé að lesa ýmsar upplýsingar úr þessum jöfnum getur engin séð fyrir sér lausnir þeirra fyrir almenn árekstramætti. Því er komið að því að finna lausnir. Heildisjafnan er mjög vel fallin til að finna þær fyrir almenn mætti þegar við höfum smíðað fall Greens fyrir kerfið. Það fall er óháð árekstrarmættinu, en er háð eiginleikum vírsins og inniheldur upplýsingar um segulsviðið.
Í grönnum vír getur skriðþungi innbylgjunnar í stefnu vírsins tekið hvaða gildi sem er, en þverhreyfingum rafeindanna eru skorður settar. Rafeindirnar geta aðeins haft vissa þversveifluhætti. Þverhátturinn með lægstu orkuna hefur líkindadreifingu með hámark sem liggur í miðju vírsins og dofnar út til veggjana. Hættir með hærri orku leyfa fleiri sveiflur þvert á vírinn. Bæði með og án segulsviðs er hægt að aðgreina þessa þversveifluhætti frá langsbylgjunni ef ekkert árekstramætti er í vírnum. Árekstramætti verður síðan til þess að rafeind getur skipt um þversveifluhátt og þess vegna langsskriðþunga í árekstri. Í grönnum vír má búast við að aðeins nokkrir þversveifluhættir skipti máli. Því er heppilegt að varpa heildisjöfnunni á þessa hætti þannig að úr verði tengdar einvíðar heildisjöfnur, ein fyrir hvern hátt. Árekstramættið tengir þær saman og fall Greens fyrir einvíðu jöfnurnar er einfaldara að finna en fyrir tvívíðu jöfnuna.
Þetta bragð er ekki hægt að endurtaka óbreytt fyrir kerfið í segulsviði. Ástæðan er Lorentz-krafturinn sem verkar þvert á skriðþunga rafeindanna. Hann leiðir til þess að árekstrarmættið virðist óstaðbundið og háð hraða eða skriðþunga rafeindanna. Eftir því sem rafeindin fer hraðar er henni ýtt af Lorentz-kraftinum meira út í aðra hlið vírsins. Fari hún nógu hratt er því eins og hún hætti að sjá árekstrarmættið í miðju vírsins. Til þess að leysa þennan vanda verður að varpa langshniti hlutafleiðujöfnunar yfir í skriðþungarúmið áður en henni er breytt í heildisjöfnu
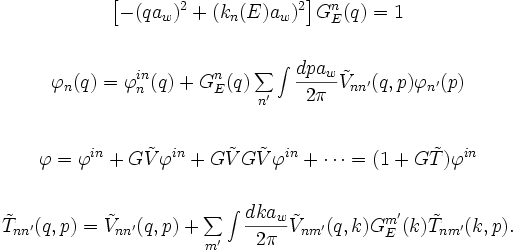
Heildisjafnan fyrir ástand-n í skriðþungarúminu er óheppileg að því leyti að innástandið er ekki bylgja eins og í staðarrúminu heldur einn mjög skarpur toppur. Til þess að leysa þann vanda er jöfnunni breytt í tengdar heildisjöfnur fyrir dreififylkið Tnn'(q,p). Þessum jöfnum er síðan breytt í fylkjajöfnu af gerðinni Ax=b, þar sem x er óþekkti vigurinn sem gefa mun Tnn'(q,p). Fylkið A er í þessum reikningum af stærðinni 400x400 upp í 6000x6000 og er búið til þannig að hluti heildunarinnar er gerður með greinireikningi í kringum sérstöðupunkta Greens-fallsins.
Leiðnin G(E) sem fall af orku innbylgjunnar er síðan reiknuð og bylgjufallið fyrir innbylgju-n með orku E
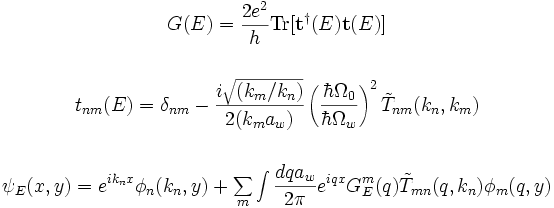
Sést þá enn ein ástæða fyrir þessari flóknu leið til þess að leysa hreyfijöfnuna fyrir rafeindirnar í kerfinu. Það er ekki mjög einfallt að reikna leiðnina þó svo við hefðum bylgjufallið eða líkindadreifinguna fyrir rafeindirnar.
Við athugum niðurstöður fyrir tvenns konar hringi í vírnum, annan lítinn en hinn stóran. Vírinn sjálfur er frekar breiður, skölunarstikinn fyrir lengd aw=33 nm hér
Leiðni vírsins með smáa hringnum sést á næstu mynd sem fall af orku innbylgjunnar. Orkan E hefur verið sköluð og er táknuð með stikanum X. Hann tekur heiltölugildi í hvert skipti sem nýr þverháttur opnast í vírnum. Ef ekkert árekstramætti væri í vírnum væri leiðnin einfallt þrepafall. Leiðnin eykst um einn leiðniskammt í hvert skipti sem nýr þverháttur opnast í vírnum. Leiðniskammturinn er ákvarðaður af náttúruföstum óháðum vírnum, hleðslu rafeindar og fasta Plancks.
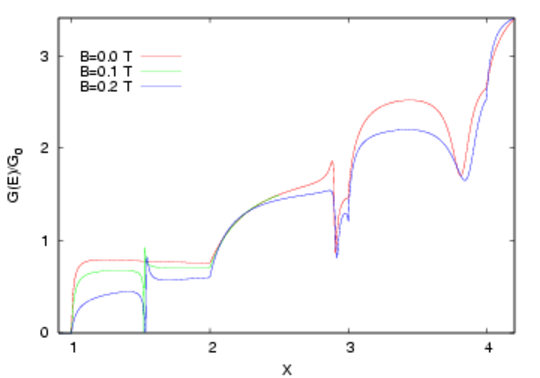
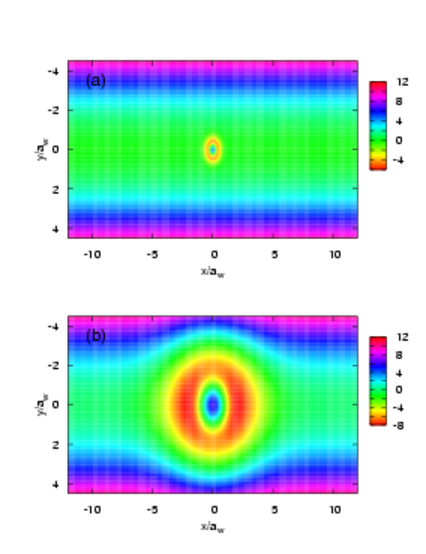
Leiðni vírsins með smáa hringnum er ekki þrepafall svo ljóst er að hringurinn hefur mikil áhrif þó hann sé smár. Lítum á líkindadreifingu rafeindanna fyrir gildi á X rétt fyrir neðan X=1.5 áður en vírinn lokast. aw=33 nm og B=0.1 T hér
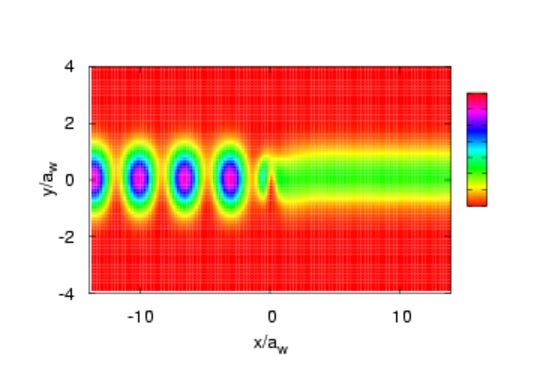
Litli hringurinn er staðsettur í miðjunni nærri x=0. Innbylgjan víxlast við spegluðu bylgjuna sem endurvarpast út til vinstri frá hringnum og myndar þannig víxlmynstrið til vinstri á myndinni. Aðeins einn þversveifluháttur heldur áfram til hægri og því sést ekkert víxlmynstur þar. Hið veika segulsvið B=0.1 T nægir til þess að rjúfa samhverfuna um langás vírsins. Við X=1.5 lokast vírinn og fyrir aðeins hærra X leiðir hann algerlega, G(E)/G0=1. Þetta er svo kölluð Fano-herma, sem verður þegar eitt af eiginástöndum hringsins lendir inn í samfellda orkurófi ástanda vírsins. Innbylgjan lendir í hermu við þessa orku og endurkastast algerlega fyrir eitt gildi X og sleppur óbreytt í gegn fyrir aðeins hærra gildi. Þetta sést best á líkindadreifingunni
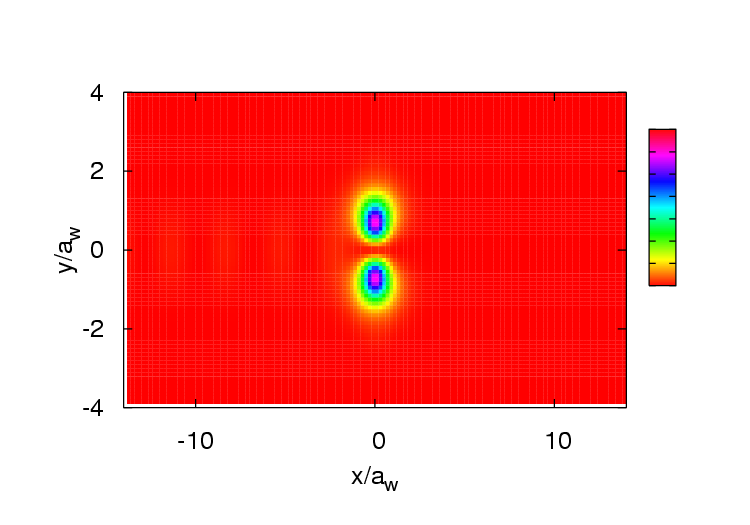
Við sjáum einungis "sama sem bundna ástandið". Rafeindin eyðir það miklum tíma þar að inn- og útbylgjurnar sjást varla. Þetta er einmitt gott dæmi um fyrirbæri sem aðeins sést vegna þess að þess var sérstaklega gætt að henda ekki í burtu endurteknum árekstrum úr reikningunum. Fano-hermur eru þekktar í atóma- og sameindakerfum en sáust fyrst í hálfleiðarakerfum 2004. Til samanburðar sést á næstu mynd líkindadreifingin fyrir samskonar hermu við hærra segulsvið
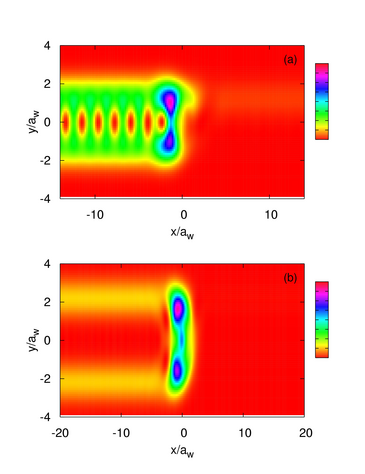
Hér sést að við hærra segulsvið B=0.6 T og 1.2 T færir Lorentz-krafturinn inn- og spegluðu bylgjuna í sundur þannig að þær víxlast ekki lengur við hærra segulsviðið.
Leiðni breiða vírsins með stóra hringinn sést á næstu mynd fyrir B=0 T og 1T
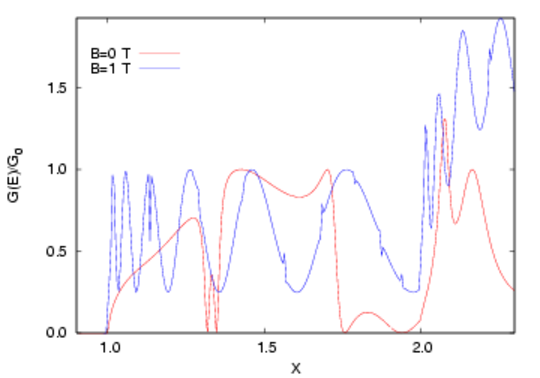
Greinilegt er að hér er annað að gerast en í smáa hringnum. eins og sést best með því að skoða líkindadreifingu rafeindanna. Skoðum fyrst 3 tilfelli fyrir B=0 T
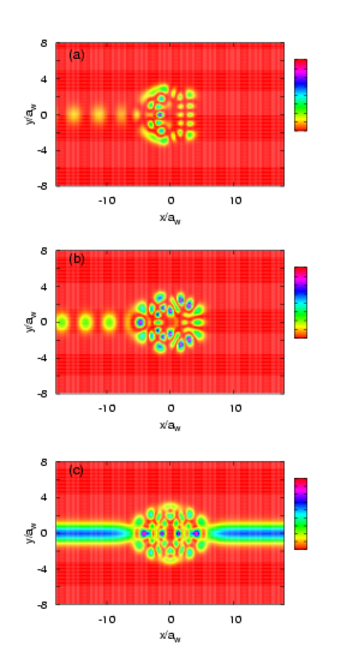
Fyrstu tvær myndirnar eiga við lokun vírsins rétt við X=1.3. Við sjáum víxlmynstur út- og spegluðu bylgjunar og mjög flókna dreifingu innan hringsins. Aftur er hér um hermu að ræða en núna er ástand hringsins sem lendir inn í samfelldu ástöndum vírsins ástand með háa orku og flókna uppbyggingu miðað við grunnástand hans. Það kom einmitt mönnum á óvart fyrir nokkrum árum hve svipuð "sama sem bundnu" ástönd opna hringsins eru bundnu ástöndum lokaða hringsins (án tengingar við vír). Á ensku er talað um "scarred wave functions" eða "persistent wave functions". Þetta hefur mikið verið rannsakað fyrir mismunandi vel opna eða lokaða skammtapunkta. Neðsta myndin sýnir líkindadreifinguna þegar engin speglun verður í hringnum. Þá er dreifingin með hægri-vinstri samhverfu og út- og innbylgjurnar eru hér með aðeins einn þversveifluhátt og þess vegna sést ekkert víxlmynstur í vírnum.
Enn athyglisverðari fyrirbæri koma í ljós fyrir B=1 T. Fyrst tökum við eftir jöfnum sveiflum sem vaxa í bylgjulengd með vaxandi orku. Þetta eru svo kallaðar Aharanov-Bohm sveiflur. Þær verða þegar bylgja hefur farið eina umferð um hringinn og víxlast eyðandi eða styrkjandi við sjálfa sig allt eftir bylgjulengd rafeindabylgjanna, sem er fall af orkunni X. AB-sveiflur eru hreint skammtafyrirbæri með enga samsvörun í sígildri eðlisfræði.
En ofan á AB-sveiflunum sjást litlar truflanir. Það þarf einmitt að athuga hvort þetta sé merki um að tölulegu reikningarnir séu að bregðast. Það var gert með því að auka nákvæmni reikninganna og í ljós kom að þetta eru raunveruleg hrif. Litlu óreglurnar eru hermur vegna eiginástanda hringsins sem lenda í samfellda orkurófi vírsins. Þetta sést best með því að athuga líkindadreifingu rafeindanna fyrir truflunina í 3. AB-toppinum og bera saman við dreifinguna fyrir 5. AB-toppinn, sem er ótruflaður
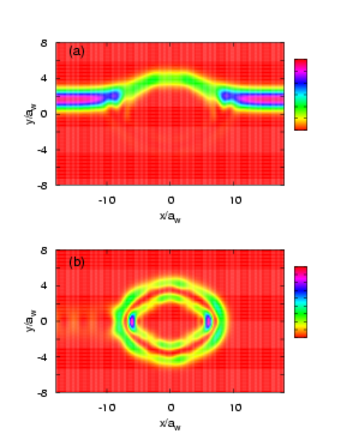
Fyrri myndin sýnir líkindin í 5. AB-toppinum. Hér sést greinilega innbylgjan sem fer aðallega hálfa umferð um hringinn og síðan út til hægri. Minna sést hlutinn sem fer heilan hring og liðast styrkjandi við innbylgjuna. Seinni myndin sýnir líkindadreifingu sem minni mjög á bundið ástand hringsins. Rafeindirnar eru nógu lengi í hringnum til þess að líkindadreifingin sjáist illa fyrir innbylgjuna í vírnum. Þó mótar aðeins fyrir víxlmynstri inn- og spegluðu bylgjunar.
Þessar rannsóknir tóku um það bil eitt og hálft ár og voru unnar í samvinnu við framhaldsnema við Háskóla Íslands og við Chiao-Tung Háskóla í HsinChu á Tævan ásamt eðlisfræðingum frá Íslandi, Danmörku, Rúmeníu og Tævan.

Til þess að ljúka tölulegum reikningum á skömmum tíma var notað reikniafl þyrpingarinnar Bjólfs sem er í eign nokkurra rannsóknahópa á H.Í. svæðinu.

En góð líkön og mikið reikniafl næga ekki. Til viðbótar þarf mikið skipulag, tilfinningu fyrir eðlisfræðilegum eiginleikum og feykilegt úthald til þess að berjast við forritunarlýs og til að sannfæra sig og aðra um gæði niðurstaðna. Þeir sem halda það út skemmta sér konunglega við þessar rannsóknir enda er fátt skemmtilegra en að sigrast á vandamálum og öðlast skilning á nýjum og þekktum fyrirbærum eðlisfræðinnar.
Niðurstöður þessara rannsókna eru eða verða birtar í ritrýndum alþjóðlegum tímaritum um eðlisfræði. Aðgengilegar eru þær í forprentaformi á vefnum:
Rannsóknirnar hafa verið styrktar af: