Dæmaskammtur 10 fyrir Aflfræði (EÐL302G) 2020

1. Kerfi er gert úr mössum sem fastir eru í hnitunum (kartíska hnitakerfi hlutarins):
   M í a(1,0,1)
   M í a(0,2,0)
   2M í a(0,-2,0)
   M í a(1,0,0)
   
   1. Finnið hverfitregðuþininn.
   2. Finnið höfuðása kerfisins.
   3. Sýnið að úr höfuðásunum er hægt að útbúa ummyndunarfylki sem setur hverfitregðuþininn á hornalínuham.


2. Hugsum okkur hjólflöt (torus) með tvo geisla R og a þannig að R > a. Gatið í gegnum hjólflötinn er með geisla (R-a) > 0. Um gatið liggur samhverfuás flatarins. Samhverfuásinn fellur saman við z-ás kartísks hnitakerfis. Reiknið hverfitregðuþininn fyrir gegnheilan hlut sem markast af hjólfletinum (kleinuhring) með massa M. Ekki nægir að skrifa niður svarið, sem vissulega má finna á vefnum.


3. Þyrill (dumbbell) liggur í eigin hnitakerfi eins og myndin sýnir:
   
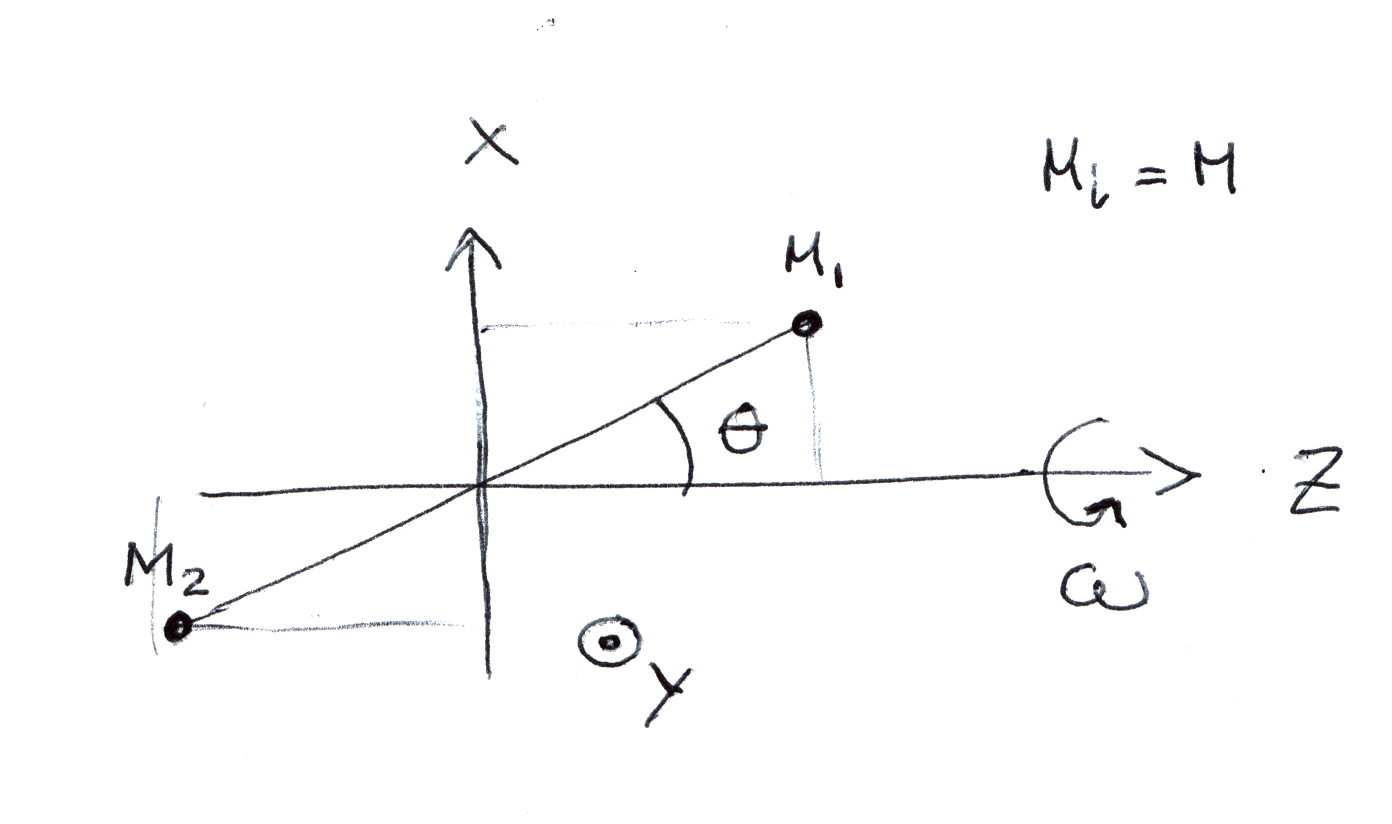
   Honum er haldið á föstum snúningi í hnitakerfi tregðukerfis sem er með z'-ás sem fellur saman við z-ás þyrilsins. θ er fast horn í kerfi þyrilsins.
   1. Finnið hverfitregðuþin þyrilsins.
   2. Finnið hverfiþunga þyrilsins út frá skilgreiningu, og út frá hverfitregðuþininum. Ber þessum niðurstöðum saman?
   3. Finnið hreyfiorku þyrilsins.
   4. Finnið vægið sem nauðsynlegt er til að viðhalda snúningi þyrilsins.


4. Kerfi er gert úr mössum:
   4M í a(0,0,1)
   M í a(0,1,0)
   M í a(1,0,0)
   
   1. Finnið hverfitregðuþininn fyrir snúning kerfisins um 0-punktinn í kartíska hnitakerfinu.
   2. Finnið massamiðju kerfisins.
   3. Finnið hverfitregðuþininn fyrir snúning um massamiðjuna.