Dæmaskammtur 05 fyrir Aflfræði (EÐL302G) 2020

1. Hugsum okkur lóðréttu x-z-sléttuna. Ögn með massa m fellur í þyngdarsviði viðnámslaust eftir braut sem er lýst með fallinu x = a*sin(kz), þar sem k > 0 og a > eru fastar með víddir [a] = L, en [k] = 1/L. Ögnin fellur úr punktinum z = 0 klukkan t = 0.
   1. Hvernig getum við lýst skorðum leiðarinnar?
   2. Finnið hreyfijöfnur Lagrange fyrir ögnina þegar beint tillit er tekið til skorðanna. Hve mörg alhnit eru nauðsynleg?
   3. Finnið hreyfijöfnur Lagrange fyrir ögnina með því að nota skorðufallið með margfaldara Lagrange λ. Hve mörg alhnit þarf?
   4. Finnið fallið λ(z,ż) sem lýsir margfaldara Lagrange?
   5. Finnið x- og z-þætti skorðukraftsins sem verkar á ögnina sem fall af z og ż.
   6. Finnið víddarlausan stika sem greinilega hefur mikil áhrif á útlit lausnarinnar.


2. Athugum aftur ögn sem er í mættinu U(x) = -U₀sin²(kx/2), þar sem k tengist lengdarskalanum L með k = 2π/L, og U₀ > 0.
   1. Finnið fall Lagrange fyrir ögnina.
   2. Finnið hreyfijöfnu agnarinnar.
   3. Finnið fall Hamiltons fyrir ögnina.
   4. Finnið hreyfijöfnur Hamiltons fyrir ögnina.
   5. Finnið tíðni smárra sveiflna um eina jafnvægisstöðu agnarinnar þegar orkan E < 0 og mjög nærri -U₀.


3. Ögn með massa m hreyfist í láréttu x-y-sléttunni. Kerfinu er lýst með falli Lagrange
   
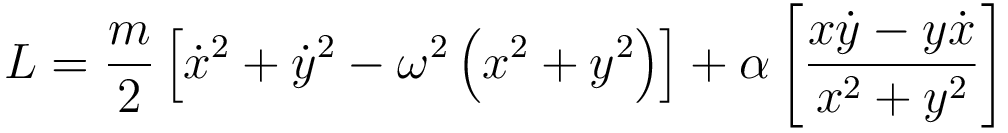
   Finnið hreyfijöfnur kerfisins. Finnið alskriðþunga þess. Er eitthvað einkennilegt við kerfið? Dæmið býður upp á góða æfingu um muninn á heildar- og hlutafleiðum í jöfnum Eulers og Lagrange, en hér er miklu meiri eðlisfræði falin, sem við skoðum í dæmatíma.


4. Leysið dæmi 06-02 í nýjústu útgáfu DC (önnur endurskoðun).