Dæmaskammtur 04 fyrir Aflfræði (EÐL302G) 2020

1. Hugsum okkur þunnan hring með geisla a og massa M sem liggur í x-y-sléttunni með miðju í miðju hnitakerfinu. Árið 2015 reiknuðum við þyngdarmættið Φ(R) frá hringnum í sléttu hans í fjarlægð R >> a með liðun. Núna reiknum við Φ(R) allstaðar í sléttunni. Þægilegt er að vita af heildi 3.617 í Gradsteyn og einfalda það:
   
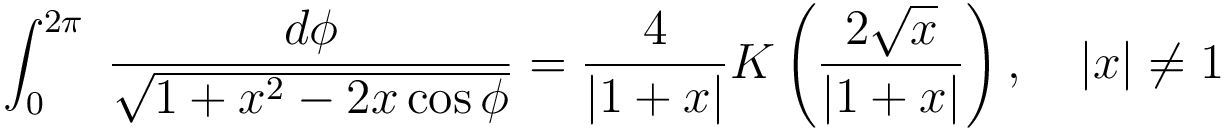
   Fyrsta fullkomna sporbaugsheildið K(k) er til í gnuplot sem "EllipticK" og því er engin ástæða til að hræðast það. Teiknið upp mynd af nákvæmu lausninni fyrir Φ(R) í sléttunni innan og utan hrings. Bætið við 0.- og 2.-nálguninni, sem reiknuð var 2015. Hvert er gildi Φ(R) þegar R=0? Er Φ(R) fasti innan hringsins?


2. Við skoðum kúlu með geisla a og massadreifingu ρ sem er ekki háð hornunum í kúluhnitum. Þyngdarsviðið innan kúlunnar er óháð geislanum r. Hvernig verður massadreifingin ρ(r) að vera svo það standist?


3. Yfirborði er lýst með jöfnunni z = (x²)/2. Finnið skemmstu leiðina milli punktanna (0,0,0) og (1,1,1/2). Teiknið upp ferilinn í x-y-sléttunni og berið saman við beina línu.


4. Athugum útgildi
   
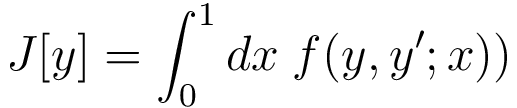
   þar sem f(y,y';x) = {((y')²)/2 - (y⁴)/4}. Finnið ólínulega afleiðujöfnu fyrir y(x) sem þið getið ekki leyst með ykkar þekkingu. Leysið hana með FORTRAN forritinu góða af vefsíðu námskeiðsins. Notið einnig forritið til að leysa línulegu afleiðujöfnuna y'' + y = 0. Grafið lausnirnar fyrir upphafsskilyrðin y'(0) = 1 og y(0) = 1. Besti samanburðurinn fæst fyrir grafið af y'(y). Lýsið niðurstöðunum. Eru þetta kunnuglegir ferlar?