Á undanförnum árum hef ég unnið með nemendum og samverkamönnum úr ýmsum áttum að lýsingu á ferð rafeinda um hálfleiðarakerfi á nanóskala. Við höfum beitt ýmsum aðferðum skammtafræðinnar til þess. Í texta hér á undan er lýsing á aðferðafræði sem byggir á dreififræði (E. scattering approach). Þar er fylgst með hvernig líkindabylgjur rafeindar koma inn í kerfið og brotna á fyrirstöðu þannig að hluti bylgnanna endurkastast út úr kerfinu eða komast í gegnum það. Fyrirstaðan er einhver breyting á mættinu (stöðuorkufallinu) sem lýsir lögun kerfisins. Leiðnin er tengd hugtakinu um líkindi þess að rafeindin komist í gegnum kerfið.
Eftir að hafa unnið með dreifilýsinguna vildum við gera betur. Hvað ef fleiri rafeindir en ein fara um kerfið samtímis? Hverju breytir Coulomb-víxlverkun þeirra? Kerfið er opið, það er, rafeindir bera hleðslu, orku og skriðþunga inn og út úr kerfinu. Kerfið er því ekki í jafnvægi. Hvernig er þannig kerfi best lýst?
Við völdum að fara leið sem kennd er við japanska eðlisfræðinginn S. Nakajima [1] og þýska eðlisfræðinginn R. Zwanzig [2] Aðferðafræði þeirra er mjög almenn fyrir opin kerfi sem eru tengd veikt við umhverfi sitt. Dreififræðin sem var nefnd hér að framan á betur við kerfi sem eru sterkt tengd við umhverfi sitt, eða galopin. Aðferð Nakajima og Zwanzig flokkast undir safneðlisfræði (E. statistical physics) opinna kerfa og leiðir til svokallaðarar almennrar stýrijöfnu sem lýsir kerfinu. Hún hefur í langan tíma verið notuð í skammtaljósfræði til þess að lýsa áhrifum rafsegulsviðs á rafeindir í atómum og sameindum. Ég kynni þessa aðferðafræði hér í nokkrum skrefum. Skoðum fyrst eðlisfræðilega kerfið sem við viljum lýsa.
Hugsum okkur tvær ytri leiðslur með mikinn rafeindaþéttleika. Hvor um sig er í jafnvægi við fasta spennu. Við veljum þá til vinstri til þess að vera við hærri spennu en þá til hægri. Fyrir klukkan t=0 er heildarkerfið í þremur ótengdum hlutum. Miðlægt er tvívítt rafeindakerfi sem getur innihaldið nokkrar rafeindir. Þetta kerfi er á nanóskala og rafeindunum er haldið í innilokunarmætti sem er með harða veggi í x-stefnu, en mjúka fleygbogainnilokun í y-stefnu. Rafeindirnar í miðlæga kerfinu víxlverka með krafti Coulombs, sem er fráhrindandi fyrir eindir með samskonar hleðslu. Kerfið er endanlegt að stærð og orkuástönd kerfisins í jafnvægi eru því strjál. Leiðslurnar eru hálfóendanleg tvívíð rafeindakerfi með verulegan rafeindaþéttleika og samfelld orkuróf. Vegna hás þéttleika rafeindanna og einsetulögmáls Paulis leyfum við okkur að horfa fram hjá Coulomb-víxlverkun rafeindanna í leiðslunum. Þvert á þessi 3 tvívíðu rafeindakerfi hugsum við okkur einsleitt fast segulsvið (í z-stefnu). Hátt segulsvið getur leitt til verulegra hleðslustrauma á jöðrum kerfanna, jaðarstrauma, en við munum aðeins athuga lágt segulsvið hér, B=0.1 T.
Við viljum staðsetja tvívíða rafeindakerfið inni í ljóseindaholrúmi (aðeins miðlæga kerfið). Við höfum t.d. áhuga á að byrja með kerfið tómt af rafeindum í upphafi klukkan t=0, en með vissan fastan fjölda af ljóseindum sem mynda standandi bylgju milli veggja holrúmsins og komast ekki út fyrir það. Klukkan t=0 eru leiðslurnar tengdar við kerfið. Rafeindir geta þá flætt inn í kerfið og hlaðið það. Eftir að kerfið hefur hlaðist gætum við búist við straum í gengum það vegna spennumunar leiðslanna.
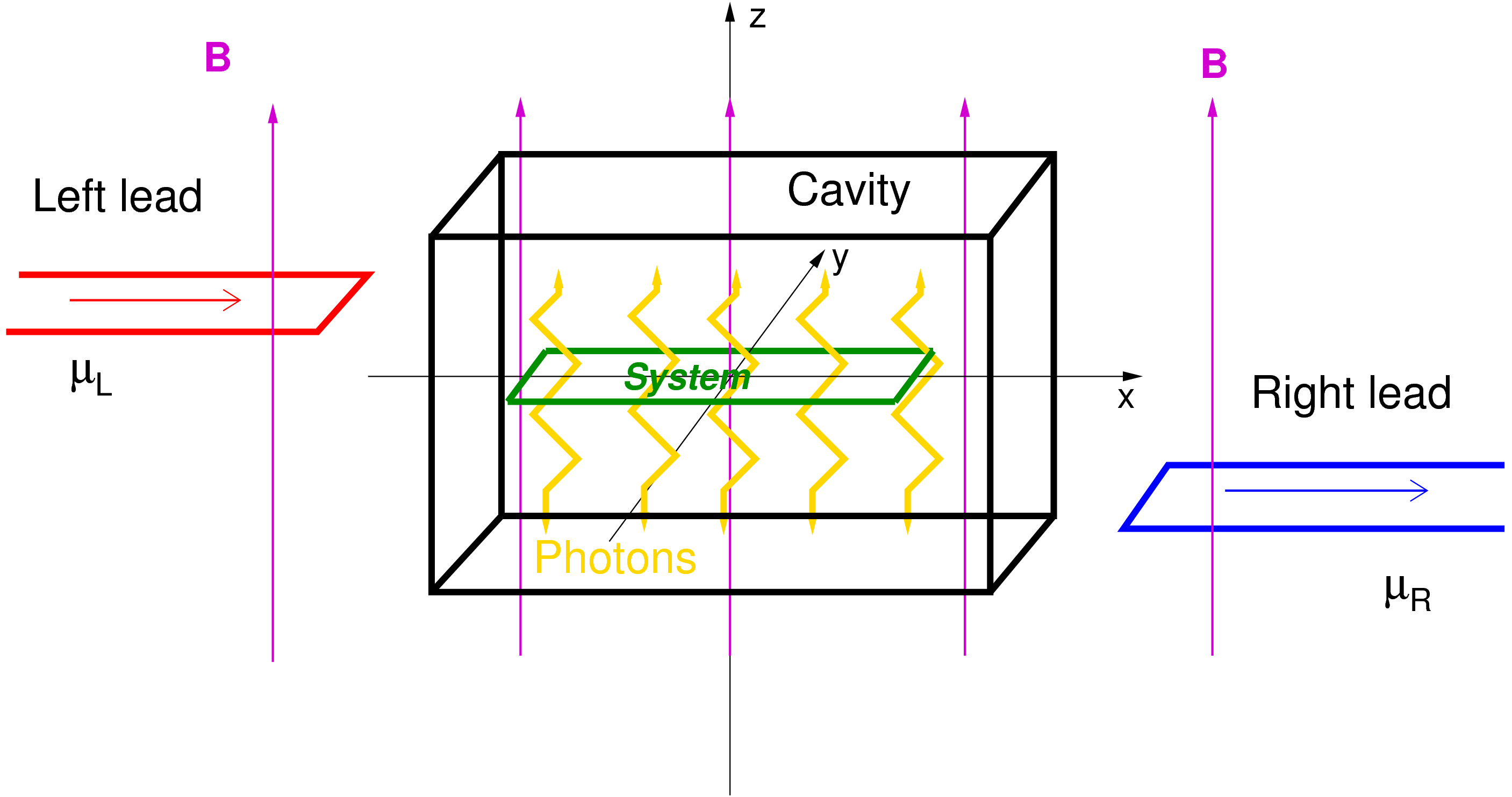
Einfaldara er að lýsa lokuðu rafeindakerfi, en opnu. Við skulum því byrja með því að kanna hvernig við getum lýst miðlæga lokaða kerfinu og að lokum notum við aðferð Nakajima og Zwanzig til þess að opna það með tengingu við leiðslurnar klukkan t=0.
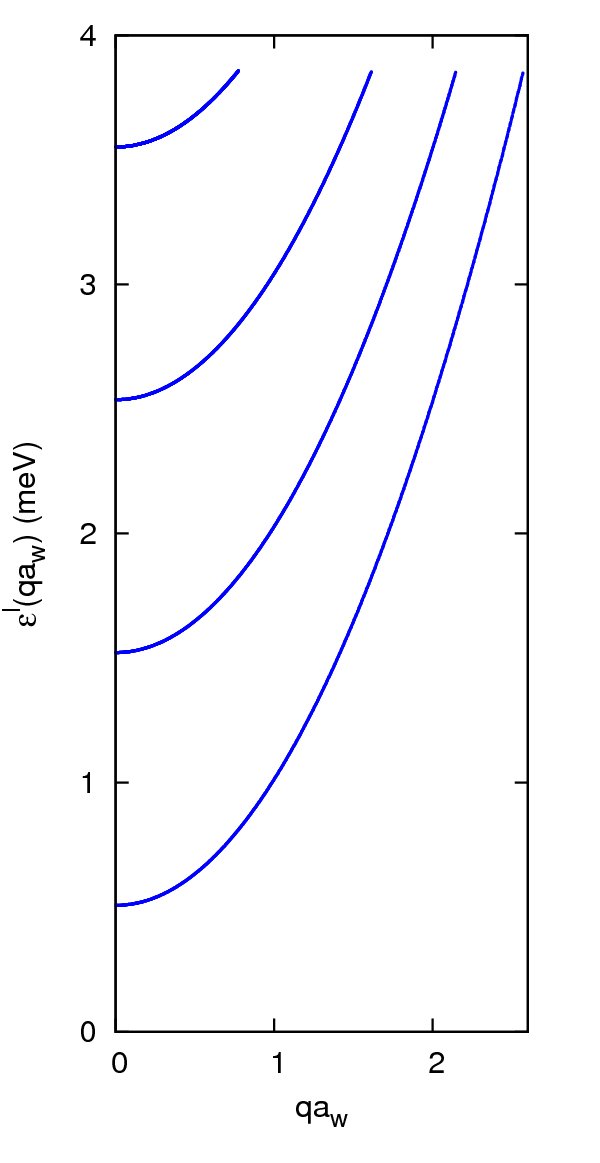

Orkurófið fyrir ytri hálfóendanlega leiðslu er sýnt hér að ofan til vinstri. Ástöndum rafeindanna svipar til standandi bylgna, þannig að hvert ástand hefur jafn mikinn skriðþunga í sitthvora áttina langs eftir leiðslunni, ±ħq. Ástöndin safnast saman í samfellda orkuborða. Hreyfing rafeindanna þvert á leiðsluna er skömmtuð. Öll ástönd lægsta orkuborðans lýsa frjálsi hreyfingu eða standandi bylgju eftir leiðslunni, en hreyfingin þvert á leiðsluna er lægsti sveifluháttur innilokunarmættisins sem lýsir lögun leiðslunnar í þá átt. Annar borðinn er myndaður af ástöndum sem öll tilheyra fyrsta örvaða sveifluhættinum þvert á leiðsluna. Óvíxlverkandi rafeindabylgjunum í leiðslunum er því lýst á samsvarandi hátt og rafsegulbylgjum í bylgjustokki.
Í rafeindakerfinu inni í ljóseindaholrúminu geta verið nokkrar víxlverkandi rafeindir. Til að lýsa því byrjum við á að finna eiginástönd einnar rafeindar í því kerfi (S) án víxlverkunar við ljóseindir. Kerfið (S) er í ytra segulsviði B og því er jafna Schrödingers ekki aðgreinanleg þar. Við leysum jöfnuna ekki á neti, en veljum að leysa hana í fullkomnu fallarúmi staðlaðra hornréttra eiginfalla aðeins einfaldara kerfis. Eiginföllin verða því samantekt þessara einfaldari eiginfalla
ψi(x,y) = Σ{nxmy}ci,{nxmy} φnx(x)θmy(y).
Eina nálgunin sem er gerð er að óendanlegu summurnar yfir nx og my eru takmarkaðar. Við köllum það að skerða eða stýfa grunninn. Stýfingin er gerð þannig að valin eru nógu há efrimörk summanna til þess að orkuróf þeirra eiginfalla sem við höfum áhuga á breytist ekki sýnilega þó aðeins sé bætt í summurnar. Ef við veldum að nota net hér í staðarrúminu til þess að leysa jöfnuna á er líklegt að einfaldara væri að skipta um lögun og gerð miðlæga kerfisins, en fallagrunnurinn er valinn því hann leiðir til þéttra meðalstórra fylkja sem einfalt er að nota almenn forrit fyrir línulega algebru sem til eru fyrir samhliða vinnslu.
Við erum þá komin með eiginföll stakrar rafeindar og þurfum að byggja upp fjölrafeindaástönd. Fallarúmin sem notuð eru til að byggja upp eiginföll stakra rafeinda eru kölluð Hilbertrúm eftir þýska stærðfræðingnum David Hilbert. Við notum svo kallaða "aðra skömmtun" og umbreytum jöfnu Schrödingers fyrir bylgjuföll yfir í jöfnu fyrir fjöleindaástönd í svo kölluðu Fockrúmi, sem nefnt er eftir rússneska eðlisfræðingnum Vladimir Aleksandrovich Fock (Влади́мир Алекса́ндрович Фoк).
Tímaháða jafna Schrödingers fyrir fjöleindaástandið ástandið 〡ψ〉er
iħ∂t〡ψ〉= H〡ψ〉,
þar sem H er virki Hamiltons sem lýsir tímaþróun kerfisins og orku þess. Til þess að lýsa tímaþróun kerfisins er heppilegt að finna fyrst eiginástönd H í Fockrúminu og orkuróf þeirra. H er abstrakt virki í flóknu óendanlega víðu ástandarúmi. Með því að velja vist ástandarúm og tilheyrandi fallarúm getum við "útsett" virkjann í því rúmi sem óendanlega stórt fylki. Eiginvigrar þessa fylkis eru eiginástönd kerfisins og eigingildi þess eru orkuróf hans. Eiginvigrarnir eða ástöndin eru háð útsetningunni, en ekki orkurófið. Það er óháð útsetningu. Til eru einoka ummyndanir milli útsetninganna. (Hér geta komið upp mikilvæg vandamál sem við skautum fram hjá). Hamiltonvirkinn okkar er settur saman úr nokkrum þáttum: H=H0+HCoul+HL,R+HEM+He-EM+HT, þar sem H0 er virkinn fyrir Óvíxlverkandi rafeindir í ytra segulsviði, HCoul lýsir verkun Coulombkraftsins í kerfinu, HL,R lýsir rafeindunum í leiðslunum, HEM lýsir óvíxlverkandi ljóseindum, He-EM lýsir víxlverkun rafeinda og ljóseinda, og HT lýsir því hvernig rafeindir úr kerfinu (S) geta smogið yfir í leiðslurnar og öfugt.
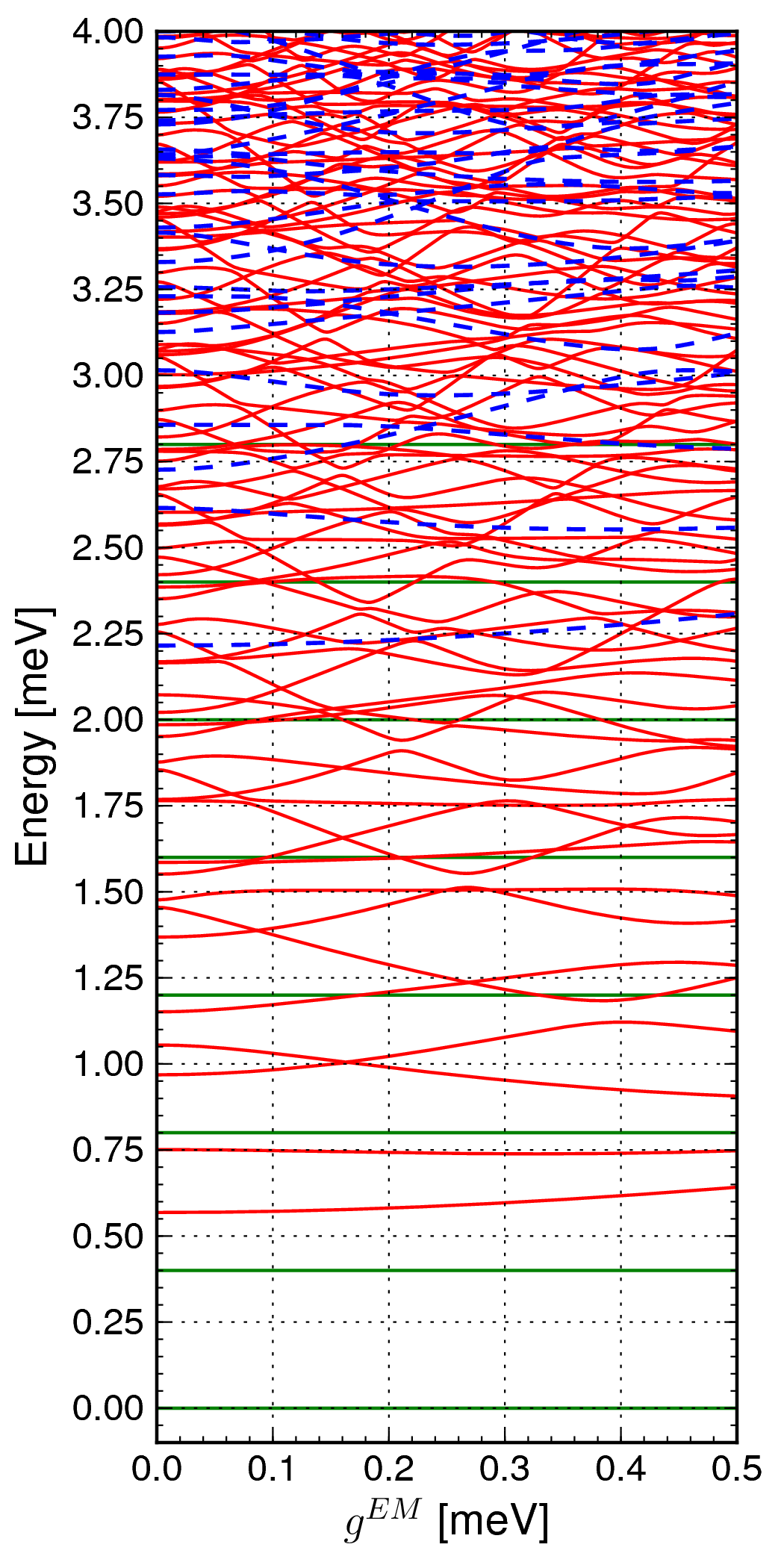
Til þess að ráða við verkefnið að finna orkuróf og ástönd lokaða kerfisins (án HT) verðum við að ráðast á það í nokkrum skrefum. Fyrst útsetjum við H0+HCoul í óvíxlverkandi Fockgrunninum og finnum orkuróf og ástönd þessa virkja, Coulombvíxlverkandi rafeinda í lokuðu kerfi. Síðan notum við einoka ummyndun til þess að umskrifa afganginn af H í þessu nýja ástandarúmi. Næst er bætt við ljóseindunum og víxlverkuninni við þær, HEM+He-EM, og nýtt ástandarúm og orkuróf fundið. Myndirnar hér að ofan, í miðið og til hægri, sýna fjöleindaorkuróf þessa lokaða kerfis sem fall af víxlverkunarstyrk gEM rafeindanna og ljóseindanna. Grænu láréttu línurnar sýna orku ástanda sem einungis innihalda ljóseindir og engar rafeindir. Þess vegna breytist orka þeirra ekki með gEM. Lægsta græna línan er grunnástand kerfisins, það er tóma ástandið með engar rafeindir, og meðalfjöldi ljóseinda er 0, en núllpunktshreyfingar skammtaða rafsegulsviðsins leiða til ljóseindaflökkts sem hefur áhrif á kerfið. Rauðu ferlarnir sýna orku ástanda sem innihalda eina rafeind og einhvern fjölda ljóseinda. Bláu ferlarnir sýna orku ástanda sem innihalda tvær rafeindir og einhvern breytilegan fjölda ljóseinda. Rafeindafjöldinn er alltaf fastur því kerfið er lokað, en ljóseindafjöldinn er breytilegur vegna þess að rafeindir geta hoppað milli ástanda með því að gleypa eða senda frá sér ljóseind. Ef við settum rafeind eða rafeindir inn í kerfið (S) verður víxlverkunin milli ljóseindanna og rafeindanna til þess að nýjar sýndareindir myndast. Þær eru samsettar úr vissum fjölda rafeinda og breytilegu hlutfalli af skömmtuðu rafsegulsviði, þ.e. ljóseindum.
Nú er komið að því að opna kerfið, tengja það við ytri leiðslur. Við erum búin að sjá orkuróf einangraðrar leiðslu lýstri með Hamiltonvirkjanum HL,R vinstra megin í myndinn hér að ofan. Þar sáum við að orkurófið er þétt í borðum. Hér kemur að safneðlisfræðinni. Ef leiðslurnar væru með endanlegan fjölda strjálla ástanda þá myndi rafeind í orkuháu ástandi í kerfinu (S) sem smygi yfir í leiðslu mjög líklega koma aftur inn í kerfið eftir endanlegan tíma. Ef leiðslurnar eru með þétt ástönd er mjög ólíklegt að slíkt hendi. Rafeindin fer úr kerfinu og við gætum metið meðalæfi hennar þar. Allir hlutar Hamiltonvirkjans H eru hermískir eða sjálfoka og leyfa ekki lausn sem sýnir meðalæfi ástands. Það er aðeins vegna víxlverkunarinnar HT við stórt ytra kerfi HL,R sem þetta getur gerst. Í skammtaljósfræði er hægt að reikna meðalæfi atómástands vegna tengingarinnar við skammtað rafsegulsviðs, ljóseindasviðs, með þétt orkuróf. Einfaldur truflanareikningur af hvaða stigi sem er fyrir rafeind í atómi hefði aldrei leitt til meðalæfi.
Tímaþróun fjöleindakerfis er best lýst með hreyfijöfnu fyrir svo kallaðan líkindavirkja W. Líkindavirkinn getur lýst kerfinu í jafnvægi eða fjarri því. Hann inniheldur upplýsingar um sætni og fylgni allra ástanda kerfisins. Jafna Schrödingers lýsir aðeins þróun eins ástands í einu. Tímaþróunarjafna W er kölluð jafna Liouville og von Neumans
iħdtW(t)= [H(t),W(t)].
Nákvæm lausn hennar er ómöguleg vegna þétta orkurófs leiðslanna. Þess vegna notum við áðurnefndar hugmyndir Nakajima og Zwanzig [1,2]. Hreyfijöfnunni fyrir W er varpað á kerfið (S) og leiðslurnar (L,R) með því að taka sporið af henni með tilliti til allra breytna leiðslanna. Við skilgreinum skerta líkindavirkjann ρS(t)=TrL,R{W(t)}, sem lýsir tímaþróun kerfisins undir áhrifum leiðslanna. Hann lýsir eiginleikum opins kerfis sem er úr jafnvægi. Við hugsum okkur að kerfin séu tengd saman klukkan t=0, þá eru leiðslurnar tengdar við kerfið (S). Hreyfijafna skerta líkindavirkjans er
iħdtρS(t)= [HS,ρS(t)]+∫[0,t]ds Λ[t,s;ρS(s)],
þar sem HS=H0+HCoul+HEM+He-EM. Fyrsti liðurinn hægra megin í jöfnunni er tímaþróun lokaða kerfisins og annar liðurinn eru áhrif ytri leiðslanna á tímaþróunina. Sá liður leyfir orku- og eindatap eða gróða. Hann er mjög flókinn liður sem opnar kerfið og gefur kerfinu minni. Ástand kerfisins á hverjum tímapunkti t er háður fyrri sögu þess. Jafnan er í raun stórt hneppi tengdra afleiðu-heildisjafna sem við þurfum að leysa. Hingað til hefur engin nálgun verið gerð fyrir tímaþróunina, nema að við setjum skerta líkindavirkjann út í stýfðum grunni fjöleindaástanda. Til þess að leysa jöfnuna verðum við að nálga fellið Λ. Við gerum það þannig að annars stigs liðir fyrir HT eru teknir með. Þar sem jafnan hefur uppbyggingu heildisjöfnu þýðir það samt að rafeindafærslur milli kerfisins (S) og leiðslna (L,R) koma fyrir í mjög háu veldi í lausninni, en við horfum fram hjá atburðum sem krefjast samsmugs (E. cotunneling) tveggja rafeinda inn eða út úr kerfinu. Það þýðir að tvær rafeinda geta vissulega farið úr eða í kerfið, en þær gera það ekki samtaka.
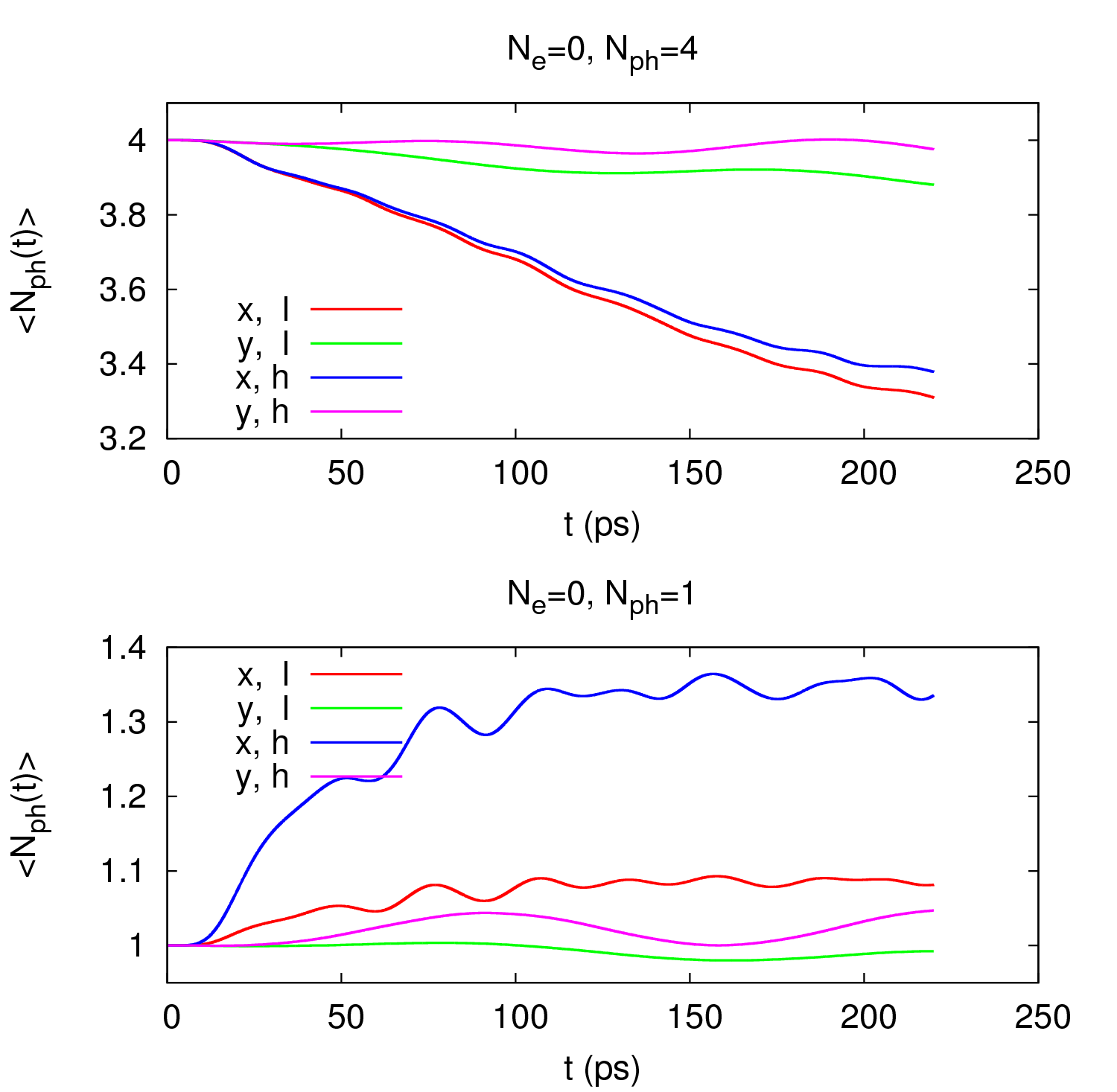
Nú veljum við forspennu milli vinstri og hægri leiðslu og reiknum tímaþróun kerfisins þegar í því klukkan t=0 er engin rafeinda en engin eða nokkrar ljóseindir. Nákvæmari lýsing á upphafstikum, kerfinu og líkaninu má finna í [3]. Næsta mynd hér að neðan til vinstri sýnir líkindi meðalfjölda rafeinda í kerfinu (S) sem falli af tíma t fyrir mismunandi ljóseindafjölda í upphafi og mismunandi skautun ljóseindanna langs eftir kerfinu í flutnings átt (x-skautun) eða þvert þar á (y-skautun). Aukinn ljóseindafjöldi virðist tefja hleðslu kerfisins. Ljóseindirnar dreifa rafeindunum út úr forspennuglugganum milli víranna, en það eru einmitt ástöndin innan hans sem leiða best í kerfinu. Myndirnar hægra megin sýna heildar meðalljóseindafjöldann sem fall af tíma, efri myndin fyrir upphaflega 4 fjóseindir í kerfinu og sú lægri fyrir eina ljóseind upphaflega í kerfinu. Í kerfinu með 4 ljóseindir virðist sem þeim fækki með tíma. Þær örva rafeindir í hærri orkustig. Það öfuga gerist fyrir kerfið með eina ljóseind upphaflega. Þar fjölgar ljóseindunum við að rafeindir fara á lægri orkustig. Mikill munur er á skautunarstefnum ljóseindanna. Það er vegna þess að orka ljóseindanna er nærri orkumun á rafeindastigum sem lýsa hreyfingu rafeinda eftir kerfinu í x-átt.
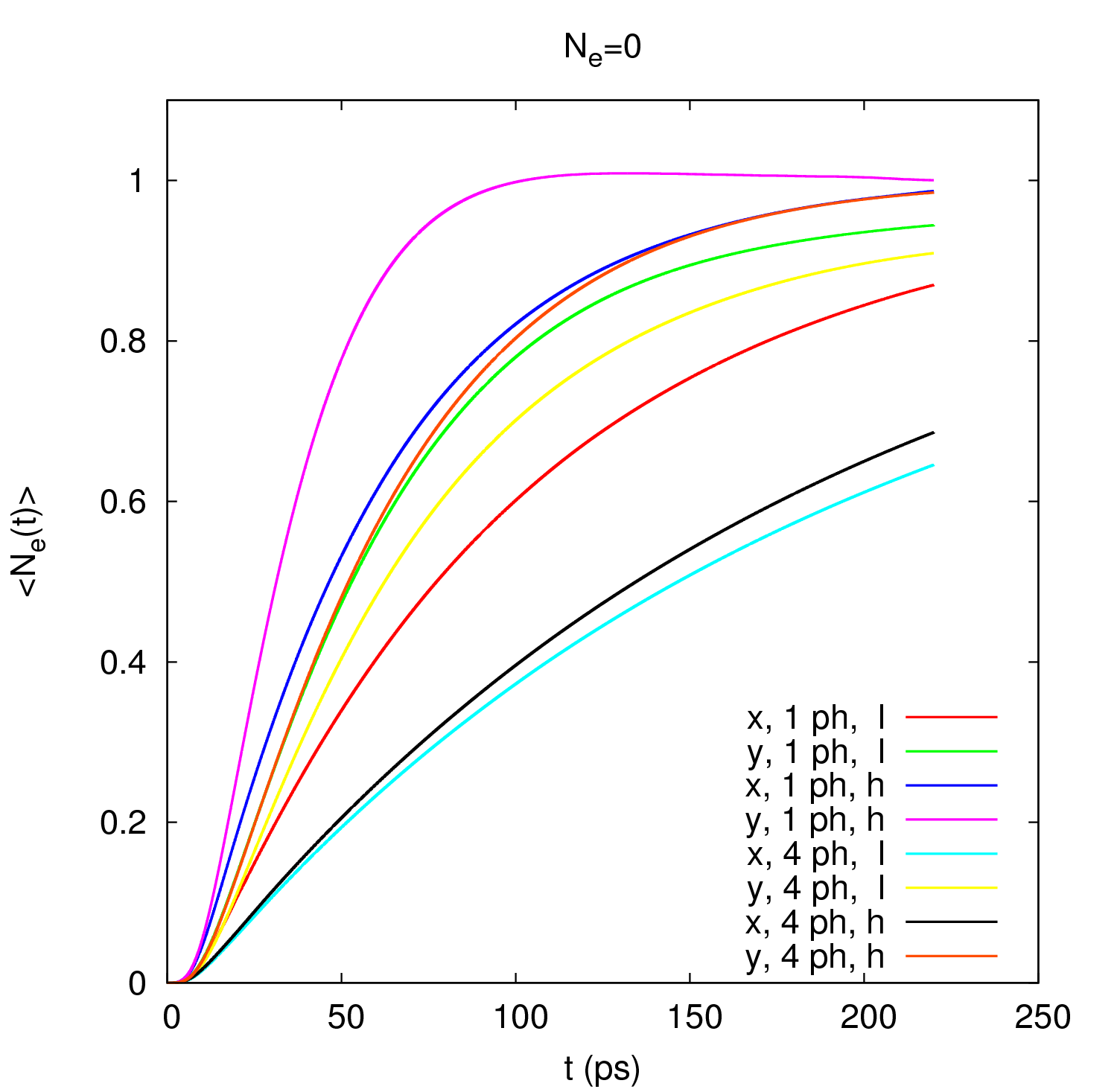
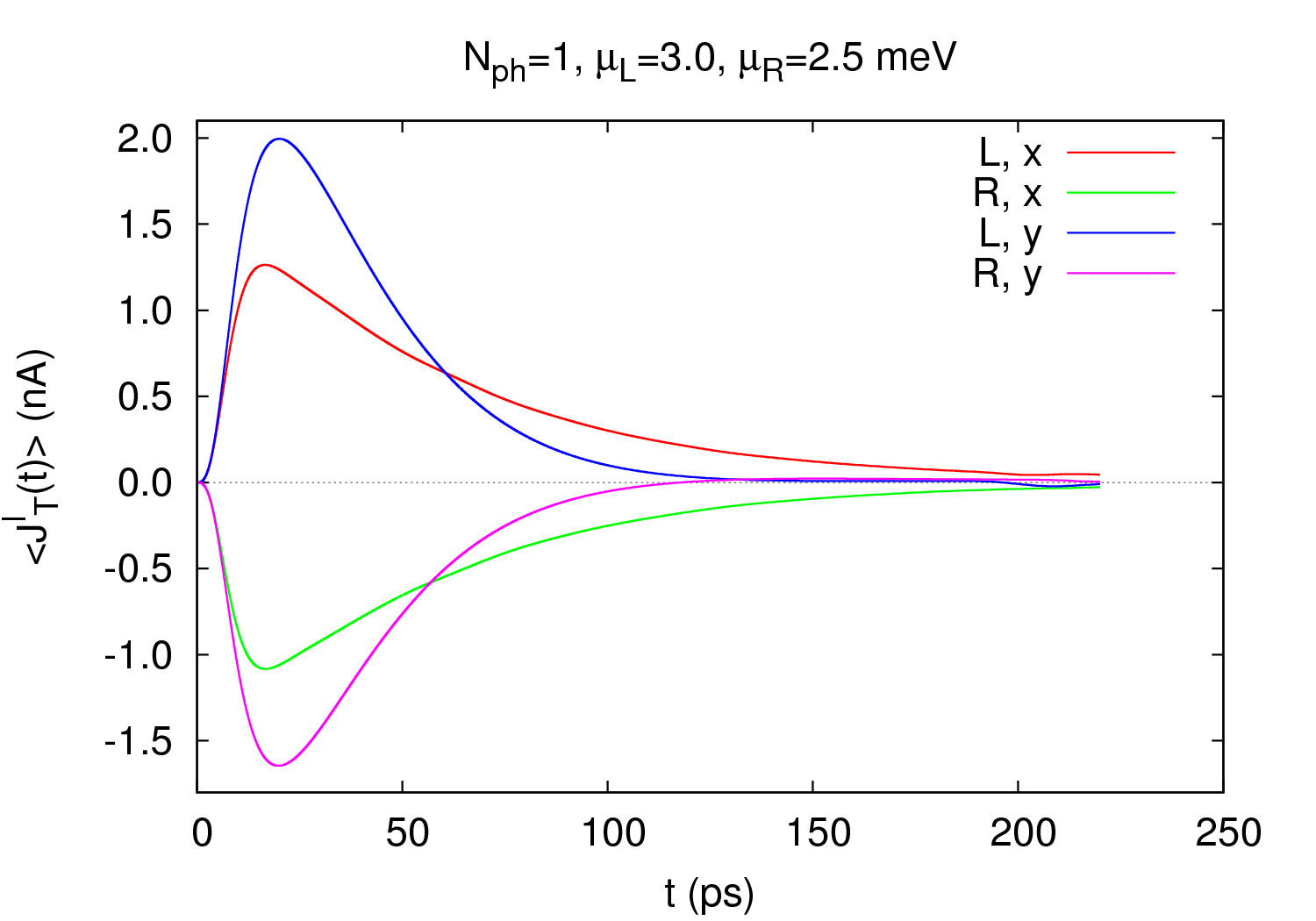
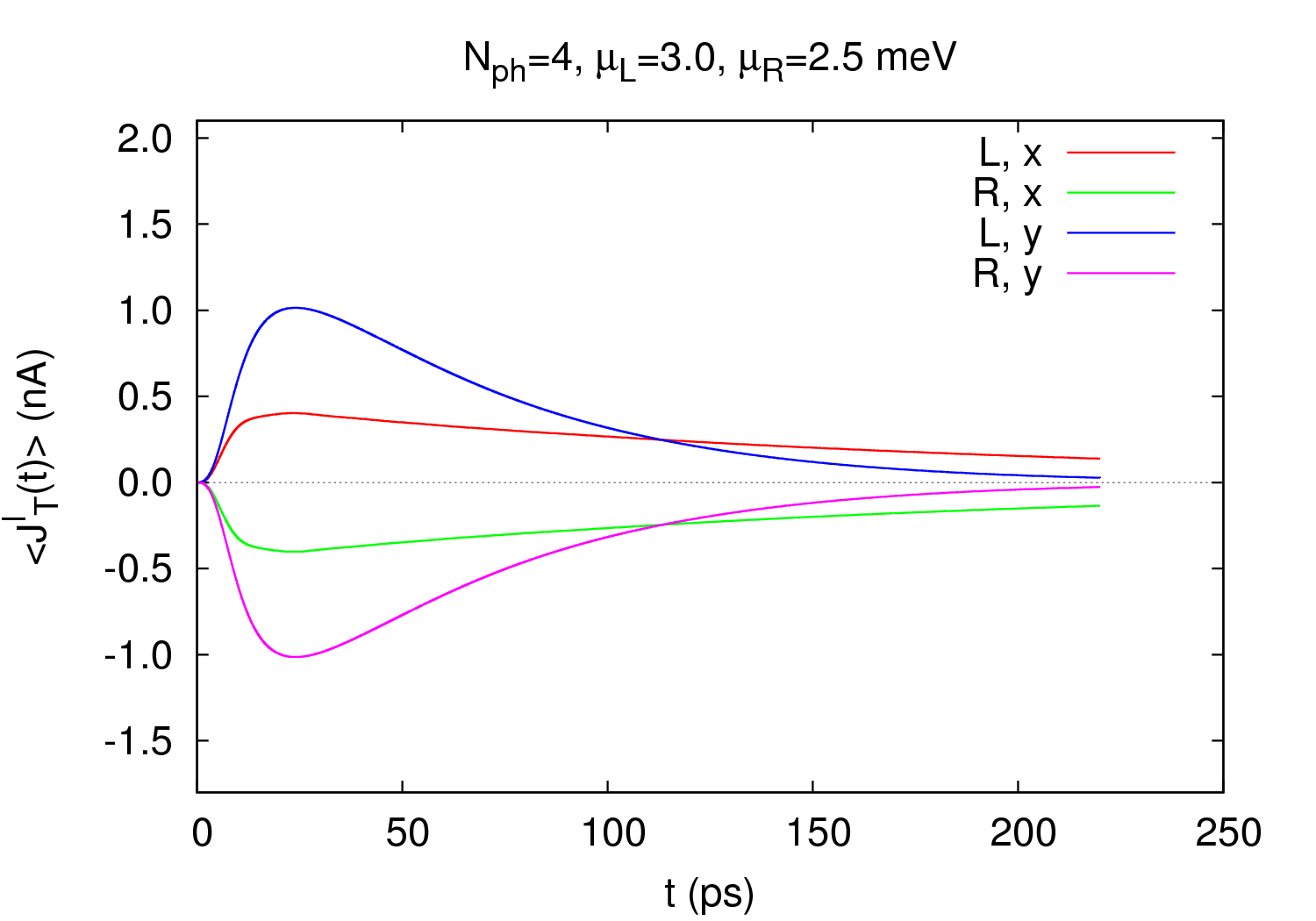
Á næstu tveimur myndum eru heildarstraumarnir inn í kerfið vinstra megin og út úr kerfinu hægra megin sýndir sem fall af tíma fyrir mismunandi upphaflegan ljóseindafjölda í því. Í upphafi eru engar rafeindir inni í kerfinu. Þess vegna flæða rafeindir inn í það frá báðum áttum og hægri straumurinn JR er neikvæður í upphafi. Hér virðast straumarnir stefna á gildi sem gefa til kynna engan heildarstraum í gegnum kerfið þegar kerfið er komið í stöðugt ástand. Þetta er vegna þess að kerfið er lítið og rafeindin í kerfinu kemur í veg fyrir að sú næsta komi inn í það. Fyrirbærið kallast Coulomb-lokun. Hægt er að yfirvinna hana með hærri forspennu á kerfið.
Hér að neðan eru myndir sem sýna líkindi þess að hleðsla (rafeind) sem kemur inn í kerfið setjist í fjöleindaástand 〡μ〉. Kerfið er í upphafi án rafeinda en með eina ljóseind, þ.e. að ástand 〡2〉er setið í upphafi. Myndirnar eru fyrir mismunandi skautunarstefnu ljóseindarinnar. Dreifing líkindanna í ástöndin sýna vel að kerfið er ekki í jafnvægi.
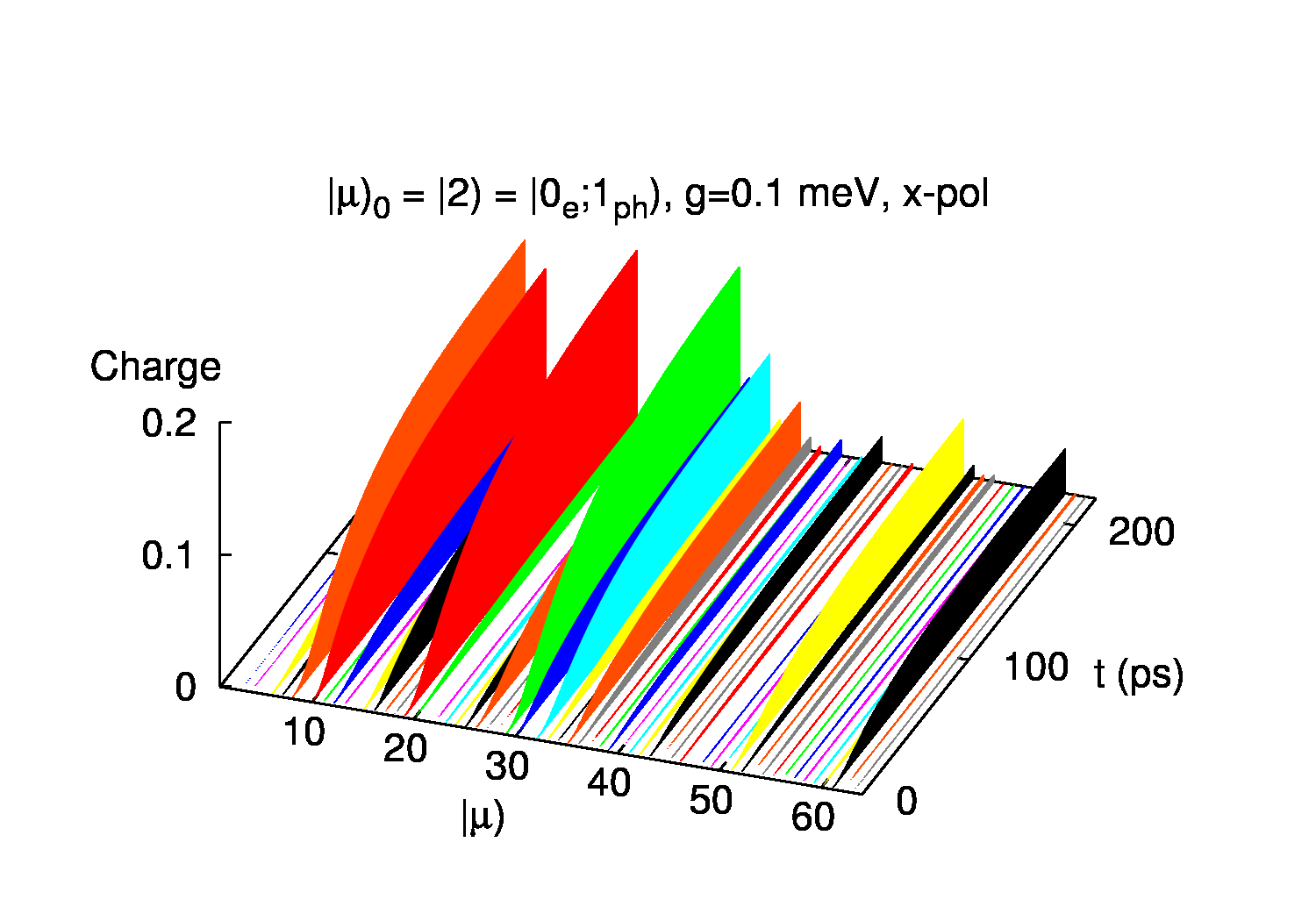
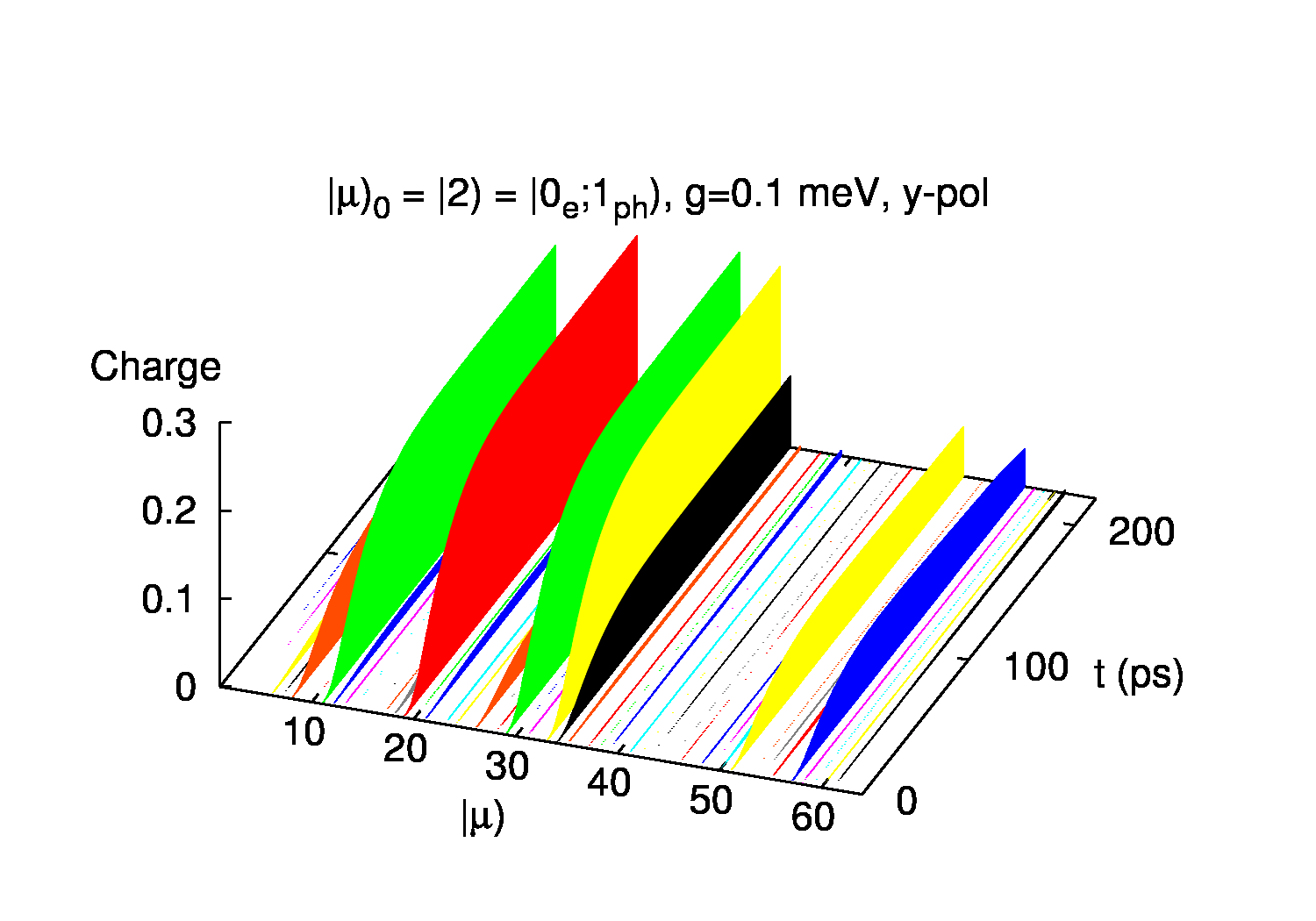
Að lokum er sýnd dreifing ljóseindanna í fjöleindaástöndin 〡μ〉. Upphaflega er ein ljóseind í kerfinu og aðeins ástand 〡2〉setið sem lýsir einmitt því. Í upphafi þegar rafeindastraumurinn er hár inn í kerfið víxlverka ljóseindirnar og rafeindirnar hratt og setja mörg mismunandi ástönd sem flest standa fyrir sýndareindir samsettar úr ljós- og rafeindum.
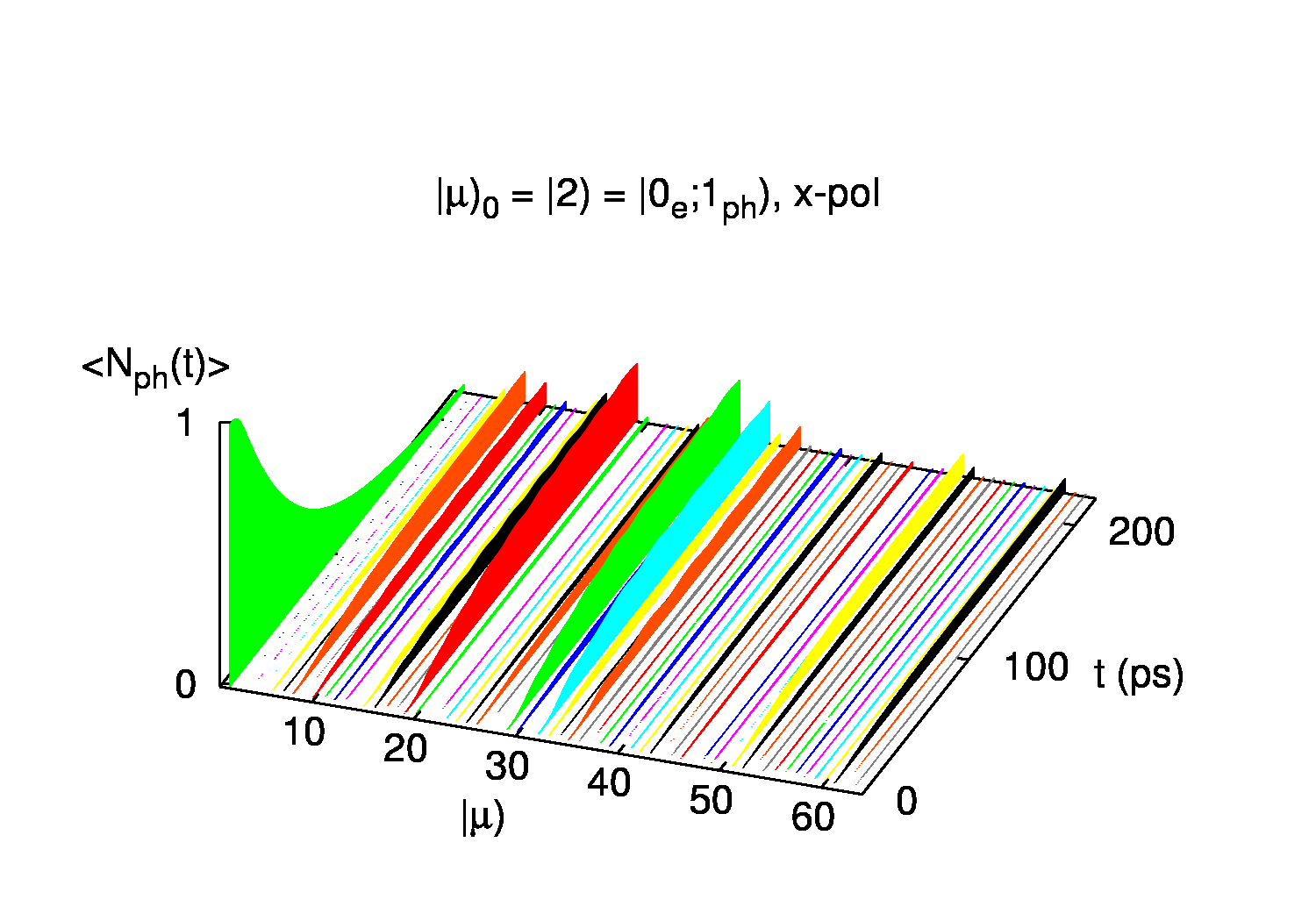
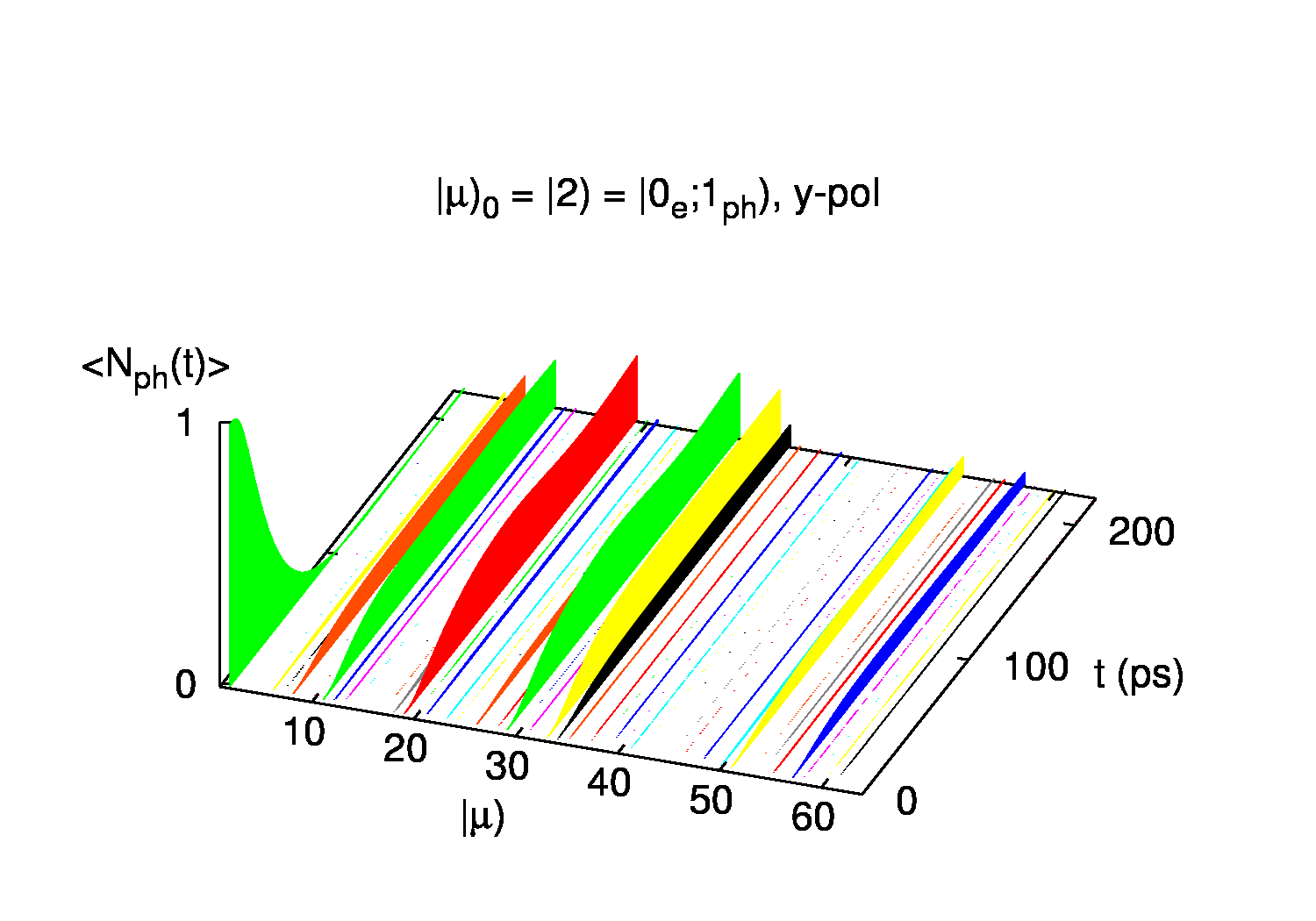
Ég veigra mig við að kalla sýndareindirnar skauteindir. Það hugtak er frekar notað fyrir örvun rafeindar eins og örveind (samband rafeindar og holu) sem víxlverkast sterkt við ljóseindasvið. Svipað gerist hér nema hvað "örveindin" er öll innan leiðniborða kerfisins (S).
Víxlverkandi rafeindakerfi í ljóseindaholi falla undir grein eðlisfræði og rafmagnsverkfræði sem fást við skammtarafsegulfræði rása (E. circuit-QED). Þau er hægt að búa til á mjög mismunandi hátt, þó aðeins einn sé nefndur hér. Einnig er hægt að nota merkjaflutingslínur og ofurleiðandi málmbúta. Hér er aðeins tekið tillit til eins ljóseindahátts. Hleðsludreifing rafeindanna í kerfinu bregst við ljóseindunum í kerfinu. Við getum kallað það skautun hleðsludreifingarinnar eða litið á það sem skýlingu á ytra rafsegulsviði. Ef fleiri en einn ljóseindaháttur væru í kerfinu væri líka hægt að athuga hvernig ljóseindadreifingin bregst við rafeindum sem koma inn í kerfið.
Þessi kerfi eru athyglisverð vegna þess að þau bjóða upp á þann möguleika að stýra leiðni með ljósi, eða öfugt. Fyrirbæri sem gætu komið að notum í skammtatölvur og önnur rafljóseindatól. Eins eru þau skemmtilegur leikvöllur til að reyna ýmis einkennileg hrif í skammtarafsegulfræði (QED) í kerfum sem leyfa breytingu á víxlverkunarstyrk ljós- og rafeinda. Í okkar rannsóknum höfum við lagt ofuráherslu á að lýsa kerfum með flókna lögun (geómetríu) og reynt að lýsa eins nákvæmlega og hægt er víxlverkun rafeindanna við ljóseindir, notandi bæði með- og andseglunarþátt víxlverkunarinnar. Eins höfum við aldrei gert ráð fyrir því að ljóseindatíðnin þurfi að vera í hermu við neina einstaka rafeindafærslu. Þetta hefur leitt til þess að við höfum þurft að eyða miklum tíma í reiknitæknilegar útfærslur og tilraunir með samhliðavinnslu verkefna á stórum CPU og GPU þyrpingum. Öll forrit fyrir reikningana hafa verið skrifuð af okkur í FORTRAN 2008, C og CUDA, önnur forritunarmál hafa ekki komið til greina vegna lélegs hraða. Reikningar á tímaþróun kerfis fyrir eitt stikasafn geta tekið frá nokkrum CPU-tímum upp í 2000 CPU klukkutíma. Reikningar hafa verið gerðir á þyrpingum Raunvísindastofnunar og á Norrænu þyrpingunni NHPC sem hýst er í Hafnarfirði.
Við höfum rannsakað þróun lokaðra kerfa sem eru örvuð í skamman eða lengri tíma með og án ljóseindavíxlverkunar [4-6]. Eins höfum við beitt líkaninu til þess að rannsaka hleðslu- og spunaflutning um skammtahring inni í ljóseindaholi [7-9], til þess að finna ljósörvaða leiðni um skammtakerfi [10], og til þess að skoða flutning vegna hitamismunar á leiðslum [11].
Hér að ofan eru tvær myndir af nokkrum samverkamönnum í þessum verkefnum.